1. Introduction
Digital Twins are used to optimize both the design and operation of complex systems. For optimizing the system design, a Digital Twin can be used to select the best between two or more competing designs, rank those designs from best to worst, or optimize parameter settings to maximize the design’s system performance. Once the system design is finalized and design parameters are optimized, the Digital Twin can be used to make state-based intelligent decisions to optimize the daily operation of the system. In design optimization, the system is configured for operation by selecting equipment, processes, operating rules, staffing levels, and so on. In operations optimization, the specific tasks to work on, resources to use, and materials to relocate are selected.
During the design phase, it is important that the Digital Twin captures variability within the system, such as variable processing times or random breakdowns. Variability has a huge impact on system performance, and if it is ignored, the results will be wrong. Hence, all experimentation and optimization during the design phase must include variability in the system.
When using a Digital Twin in an operational mode to generate a short-term plan (e.g., a production schedule), the variability must be disabled and a deterministic plan generated, which then can be regenerated when an unplanned event occurs, or a task time substantially differs from its expected time. The deterministic plan will typically be optimistic, and each time the system is rescheduled as the result of unplanned events, the performance to plan typically degrades. We can, however, assess the risk of each plan by performing a risk analysis that repeatedly generates the plan with variability enabled to provide risk measures such as the likelihood that specific orders will be on time.
In Simio, we use the term simulation run to denote a run of the model with variability enabled. Hence during design optimization, replications of a simulation run are made to capture the impact of the variability on system performance. The term plan run is used to denote a single run with variability and unplanned events disabled. Since variability is disabled, there is no need to replicate plan runs when generating schedules. However, in operation optimization, we use simulation runs and replications to analyze the risk associated with the schedule due to random variation and unplanned events.
As discussed in the following sections, Simio has many built-in features for optimizing the design and operation of complex systems. In the case of system design, it is typical to select the best from a candidate set of designs or do a search over a set of parameters to optimize the performance of a selected design. In the case of system operation, it is typical to optimize the operation of the system for a selected design. In the following sections, we will describe the Simio features for performing these optimizations.
2. Running Simulation Experiments
In general, the purpose of creating a simulation model and, subsequently, an experiment for the model is to evaluate multiple scenarios for the system. In many design applications, a set of design options have been defined, such as number of AMRs to deploy, number workers to staff for each skill set, number of storage racks, or buffer space between machines. These options are called properties of the model. Each assignment of values to these properties represents a scenario for evaluation.
Experiments are used to define a set of scenarios to be executed using the model. They are executed in batch mode with random variations enabled. This is typically done (once a model has been validated) to make simulation runs that compare one or more candidate designs for the system. Each scenario has a set of properties, such as size of each input buffer, as well as KPI’s specified as output responses, such as system throughput or buffer waiting times. The control variables are the values assigned to properties of the associated model. Since most models contain random components, such as service time distributions or random failures, replications of a given scenario are required to allow the computation of confidence intervals on the response results. Figure 1 below shows an example experiment with six scenarios, each with two properties and two responses.

Figure 1: Typical Experimentation Results
When running an experiment, each scenario is replicated a specified number of times. The number of replications to make is an important consideration since each replication produces different results based on random variation. As a result, the scenarios must be compared using statistical methods. A common statistic is a confidence interval that asserts that a given KPI will fall between an upper and lower value with a specified confidence (e.g., .95). As the number of replications of each scenario is increased, the size of the confidence intervals is reduced and thus stronger assertions about the results can be made.
Simio has several built-in tools to help analyze systems during the design phase. One of the most important features is the SMORE plot, based the work of Professor Barry L. Nelson at Northwestern University, which graphically depicts the mean, confidence interval for the mean, upper and lower percentile values, and range of each response variable. Figure 2 below shows an example of a SMORE plot in Simio.
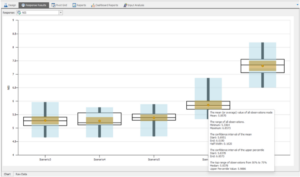
Figure 2: SMORE Plots Comparing Experiment Runs
The SMORE plot allows for visual comparison of KPIs for multiple scenarios incorporating the associated confidence intervals, which are quite helpful in determining the number of replications to run and making a first cut at selecting potentially good scenarios. However, in order to select the best scenario, we need a tool that uses a statistically valid way to select the best.
2.1 Selecting the Best System Design
In many applications, there is a set of scenarios that represent the candidate designs, and the goal is to select the best one to implement in the future based on one or more KPIs. Therefore, it is extremely important to accurately choose the best alternative(s) for the system being studied.
A simple comparison technique is to record and sort scenarios based on the average recorded KPI and then simply select the highest/lowest KPI. However, this intuitive but inexact method with no consideration of system variability may not produce the optimum choice since some scenarios may look better or worse based on random variations within the scenario set of replications. This error would have been revealed by additional replications of each scenario and more detailed analysis.
There has been considerable effort in research to develop and automate statistically valid Ranking and Selection procedures over the past several decades – a significant amount of which was done by Barry L. Nelson from Northwestern University. Dr. Nelson developed a series of algorithms that group KPI response values into the subgroups “Possible Best” and “Rejects” within each response. The “Possible Best” group will consist of scenarios that cannot be proven to be statistically different from each other but can be proven to be statistically better than all the scenarios in the “Rejects” group. This process is referred to as Subset Selection and is often done as an initial phase of analysis to create a set of “interesting” system designs to consider further.
Simio incorporates Nelson’s Subset Selection algorithm to automate this process of grouping designs into “Possible Best” and “Rejects”. To indicate what constitutes “Best”, the user defines the KPI to use as an Objective in the Response Properties window, to either Maximize or Minimize. The Maximize Objective will group the values that are statistically greater than the group of rejects, and conversely the Minimize Objective will group together the smallest response values.
When executing the Subset Selection algorithm from Simio’s Experiment window, the cells in a Response column will be highlighted yellow if they are “Rejects” leaving the “Possible Best” scenarios in brown. A scenario can have a cell in one column considered “Possible Best” and at the same time “Rejects” for another response. An example of the Subset Selection option is shown Figure 3 below.

Figure 3: Subset Selection Analysis
Simio also provides a Select the Best algorithm that automatically runs additional simulation replications as needed to select the best from a subset of “interesting” candidates. This algorithm is typically run as a second phase after the set of scenarios have been reduced to a candidate set using Subset Selection and perhaps other external factors such as cost or construction time. Simio implements the procedure developed by Seong-Hee Kim and Barry L. Nelson for selecting the best scenario. The algorithm decides which scenarios to run and how many replications of each scenario are needed to select the best. It takes an initial set of scenarios and runs additional replications until it is confident that a particular scenario is the “best”, or within a specified range of the best (called the indifference zone). It will uncheck all scenarios except for the best. As it is executing, it will “kick out” scenarios that are not a candidate for the best, and no more replications will be performed on those scenarios. This algorithm is named Select Best Scenario Using KN within Simio experimentation.
Simio also provides a second version of the Kim-Nelson algorithm that was created by Sijia Ma as part of his PhD work under Professor Shane G. Henderson at Cornell University. This version may provide improved performance when doing large scale models that require evaluation of many scenarios in a parallel processing environment. This algorithm is named Select Best Scenario Using GSP within Simio experimentation, where GSP means Good Selection Procedure as shown in Figure 4 below.

Figure 4: Select Best Scenario Options
2.2 Optimizing System Parameters using OptQuest
Simulation models are typically used within the context of a decision-making process, evaluating different possibilities for the model controls and how these possibilities affect the system. Users can manually create experiments, enter input values, and run multiple replications to return the estimated values of KPIs and their corresponding confidence intervals. This can be done by varying several different input value combinations eventually leading to an optimal solution. This method works well for simple models, but it is easy to see that it could get quite tedious as the complexity expands.
OptQuest helps remove some of the tedium by automatically searching for the optimal solution. The simulation model control properties and KPI responses are defined, along with OptQuest parameters and OptQuest then searches for the feasible control values to maximize or minimize the objective, such as maximizing profit or minimizing cost. OptQuest automatically sets the property values, starts the replications, and highlights the results.
OptQuest utilizes intelligent search methods and incorporates custom optimization algorithms alongside Simio’s modeling power. Instead of using algorithms to optimize a set of mathematical equations, it uses them to optimize a set of stochastic process interactions.
Once the problem is described by defining the control properties, objective, and constraints, OptQuest can begin running scenarios. After the first scenario, OptQuest evaluates the responses of the scenario, analyzes, and then determines values to be considered in the next scenario. After the second scenario runs, it once again analyzes the response given to it by Simio, compares it to the previous response from the prior scenario, and once again determines new values to be evaluated by Simio. This process of obtaining results and comparing to previous objective values repeats until OptQuest meets one of its terminating criteria – either after reaching the maximum number of iterations or after OptQuest has determined the objective value has stopped improving.
OptQuest also supports optimization based on more than one Response by using a technique called Multi-Objective Weighted optimization. OptQuest multiplies each objective by a specified weight, negates it is it is a Minimize object, sums them together, and the maximizes the result. An example screen of where to select and update the OptQuest parameters including an example result set is show in Figure 5 below.
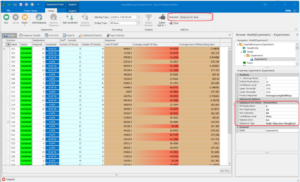
Figure 5: OptQuest Multi-Objective Weighted Optimization
OptQuest can alternatively find an optimal set of solutions based on multiple objectives using a Pattern Frontier approach, which strives for solutions that are on the “frontier” of the optimization space. For example, the following is a graph of the results for Pattern Frontier optimization with two Responses, cost, and lead time. Scenarios that lie along the optimal frontier of the solution space are shown in green in the Pattern Frontier graph and represent an optimal scenario striking a different balance between the competing objectives.

Figure 6: Pattern Frontier Graph Example
3. Optimizing System Operation
One of the key advantages of a process Digital Twin is that the same model that is used to optimize the design can also optimize the daily operations of the system by creating intelligent deterministic plans to be executed in the real system. Simio employs a state-based optimization approach to dynamically create an optimized plan that fully respects the resource, material, and logical constraints of the system as they evolve over time and are captured by the Digital Twin. Since The Digital Twin captures these true constraints of the system, the optimized plan is fully actionable in the real system. Each decision in the system is optimized based on the current state of the system. By contrast, legacy systems do not capture the detailed constraints and use a rough-cut measurement of capacity within fixed time buckets, e.g., weekly. They then employ a heuristic solver to search for a good feasible solution to this simplified representation of the system. Although legacy systems present their solution as optimal, their rough-cut approximation of both capacity and time yields results that are not actionable in the real system and, as a result, are misaligned with the actual production schedule. In contrast, Simio’s system state-based optimization approach captures all critical constraints along a true time horizon and produces a plan that is fully actionable without human intervention.
The key to the plan that is produced by the state-based optimization approach is the quality of the decision logic that is embedded in the Simio Digital Twin to make decisions such as which job to work on next, and which resources to assign to each job. In typical factories, these decisions are often made using dispatching rules, like shortest processing time, earliest due date, smallest changeover, or Critical Ratio. The Critical Ratio rule, which is the ratio of remaining time until the due date divided by the expected remaining processing time to finish the job, has been shown to be particularly effective in optimizing on-time delivery. In some cases, composite rules are employed that combine two or more rules to simultaneously reduce changeovers while minimizing tardiness. Many finite-capacity scheduling tools employ various dispatching rules to create a detailed schedule for the factory.
While these dispatching rules can generate effective schedules, a more advanced strategy involves utilizing Simio’s neural network capabilities to harness the detailed state model of the Digital Twin. These features allow for training and supplying inputs to the neural networks, enhancing intelligent decision making. With Simio, standard dispatching rules and complex model decision logic can be replaced with self-trained neural networks. The neural networks provide complex decision logic in the model, and in return the model generates the required synthetic data to train the neural networks. This allows for simplification of the model’s decision logic, which makes models easier to build, understand, debug, and maintain. Simio also provides integrated training algorithms for training neural networks using synthetic data that is generated by a model. Hence, Simio provides a complete solution for embedding neural networks in Process Digital Twin models.
Simio’s AI features are particularly useful in production planning Digital Twin applications where the neural network can be trained to predict critical KPIs, such as the dynamically changing production lead time for a factory or production line within a factory. The neural network learns the impact of changeovers, secondary resources, business rules, and other production complexities that impact the prediction of the KPIs. The intelligent Digital Twin can capture complex relationships that would otherwise be impossible to include in a model. The neural network KPI predictions can then be used to better optimize decisions, both within the factory and across the supply chain. Within the supply chain, the neural network can be used for the critical supplier sourcing decision by predicting the production lead time for each candidate supplier and selecting the lowest cost producer that can complete the order on time. AI-based factory sourcing within the supply chain Digital Twin eliminates the need for Master Production Scheduling software.
Simio’s built-in AI features provide support for defining, training, and using the classic feed forward regression neural network. However, any machine learning regression model from over 50 third parties, including Google and Microsoft, that support the ONNX model exchange format can be imported and used within Simio. Models can be built and trained within these third-party tools and then imported into Simio to create powerful AI-driven optimization solutions.
3.1 Optimizing Plans with Experimentation
The deterministic plan that is generated by the Simio Digital Twin can also be further refined by experimenting with alternate decisions within the plan. This experimentation can be done either sequentially by analyzing the KPIs for a specific plan, or in parallel to exploit multiple cores to explore many alternative plans at the same time.
Sequential refinement of a plan can be implemented using Simio’s multi-pass feature that allows a plan to be regenerated multiple times within a single run, while adjusting input parameters for each plan based on the outcomes of the previous plan. For example, if a particular job is tardy, the next iteration of the plan can change the priority of the job or send the job to an alternative production facility. This process can be repeated as necessary to refine the plan that is generated by the Digital Twin. Sequential or parallel experimentation of plans can also be implemented by running Simio in “headless” mode where it is called by a scripting language such as Python to generate specific plans. This approach is particularly useful to automatically explore different plans in parallel using multicore cloud platforms.
4. Summary
Simio Intelligent Process Digital Twins can be utilized to optimize both the design and operation of complex systems. For design applications, Simio provides advanced statistical methods for analyzing variation to optimize the system design. The same Digital Twin can then be used to optimize the daily operations of the system using a state-based optimization approach that leverages dispatching rules, neural networks, and plan experimentation to optimize performance of the system.