by Hyojung Kang, Rachel Orlowsky, and Gregory J. Gerling (University of Virginia)
As presented at the 2017 Winter Simulation Conference
In mammals, touch is encoded by sensory receptors embedded in the skin. For one class of receptors in the mouse, the architecture of its Merkel cells, unmyelinated neurites, and heminodes follow particular renewal and remodeling trends over hair cycle stages from ages 4 to 10 weeks. As it is currently impossible to observe such trends across a single animal’s hair cycle, this work employs discrete event simulation to identify and evaluate policies of Merkel cell and heminode dynamics. Well matching the observed data, the results show that the baseline model replicates dynamic remodeling behaviors between stages of the hair cycle – based on particular addition and removal polices and estimated probabilities tied to constituent parts of Merkel cells, terminal branch neurites and heminodes. The analysis shows further that certain policies hold greater influence than others. This use of computation is a novel approach to understanding neuronal development.
Introduction
The sense of touch is key to behaviors of everyday living such as feeding, social bonding and avoiding bodily harm. In mammals, touch is encoded by sensory receptors embedded in the skin (Kandel 2012). Sensory receptors include cutaneous light touch afferents as well as those signaling information regarding proprioception, chemoreception and pain. Both the sensory receptors and the skin are continually renewing and remodeling to maintain barrier in normal states and after injury (Chung 2010; Marshall 2016; Müller-Röver 2001; Rajan 2003). In hairy skin, Merkel cell nerve endings are clustered into specialized epithelial structures called “touch domes” (Plikus 2008). Mice have hundreds of touch domes in their hairy skin and humans have similar, yet subtly different nerve endings as well. More broadly, Merkel cell receptors are found throughout both hairy and glabrous skin in mammals, though local receptor and skin structures vary in each instance. In receptive populations, such afferents help to signal information regarding the edges and curvature of stimuli, among other attributes (Johnson 2001).
The dynamics of the architecture of the Merkel cell-neurite complex is just beginning to be understood (note abstraction given in Figure 1, and Lesniak 2014). A Merkel cell’s connection to or removal from a terminal neurite, and neurites from heminodes, have been observed to follow trends specific to the stages of the hair cycle in the mouse (Marshall 2016). In particular, as mice age, multiple synchronized hair cycles are observed, where the hair of the animal changes over its entire body in a wave-like fashion (Müller-Röver 2001). There are four stages of the spontaneous mice hair cycle: First Telogen: 4 weeks, Anagen: 5-6 weeks, Catagen: 6 weeks, and Second Telogen: 9-10 weeks. After this point, the hair cycle begins to enter a mosaicking phase whereby the hair over the body of the animal does not change in a wave-like fashion but instead hair is lost and regrown at different rates from seemingly random positions over the skin surface. Cutaneous neurons and Merkel cells may engage plasticity mechanisms during hair-follicle regeneration; however, the dynamics and physiological consequences of neuronal plasticity in touch receptors are not entirely understood (Moll 1996; Nakafusa 2006).
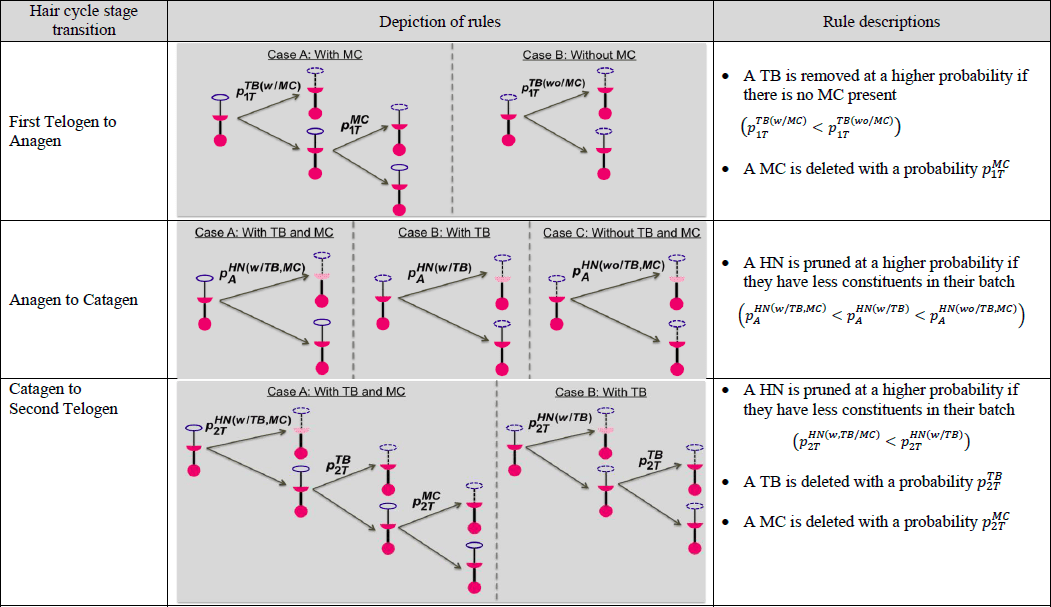
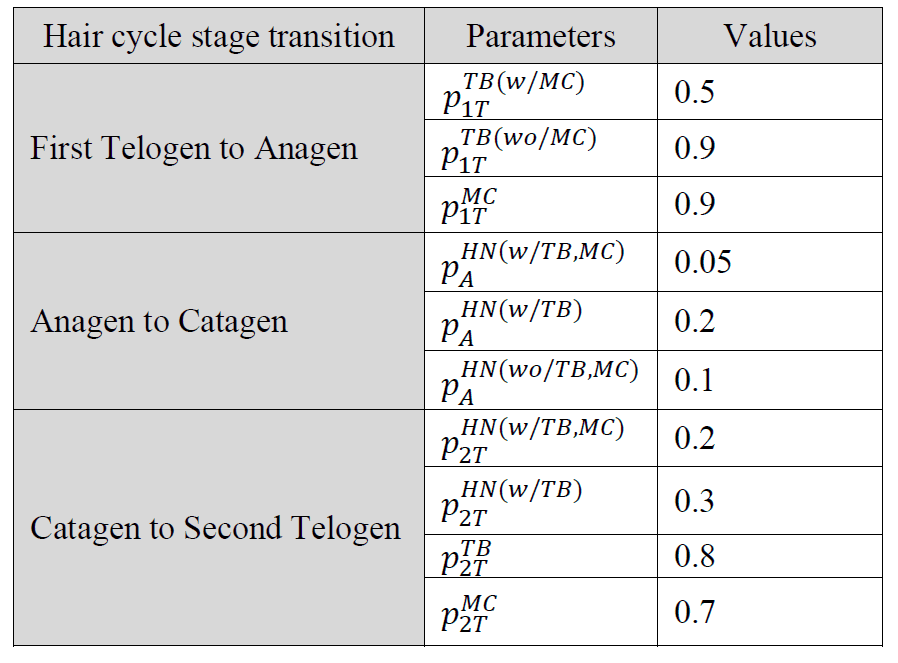
Observational research efforts regarding arbor remodeling are restricted as we are currently unable to trace specific end organs through the hair cycle. A modeling approach, in contrast, can allow for detailed traceability of end organs and each of their components through every stage of the hair cycle. Moreover, despite instances of discrete event simulation (DES) models in biological research, there are still very few published examples of comprehensively validated models. As such, our group recently built a computational model to test an initial set of rules governing arbor remodeling mechanisms (Marshall 2016). With its top down approach, population statistics from observed data were used to construct the computational model. Using the population statistics as reference points, end organ constituents were iteratively created and deleted to reflect observed data. Each of the transitions between hair-cycle stages was modeled as a separate simulation. Within each simulation, there were a number of iterations where Merkel cells and/or heminodes could be added or removed according to just four probabilistic policies, which were informed by morphometric data. That effort identified four policies of Merkel cell and heminode dynamics from observational data and evaluated the policies.
While the study (Marshall 2016) contributed to explaining rules that govern Merkel cell-neurite (or arbor) remodeling processes, those computational models have several limitations. For instance, the individual end organ constituents of Merkel cells, terminal neurites and heminodes were not traceable between phases of the hair cycle. In addition, being constrained by a top down approach hindered the formation of arbor remodeling policies central to individual components of the end organ, rather than the end organ itself. As well, because of the model structure it was not easy to perform what-if scenario tests and determine optimal parameters associated with the governing rules. Finally, there are no easy optimization or experimentation features within this model, restricting the testing of new parameters that were not previously defined. Therefore, we have sought to overcome these limitations by employing a DES approach. In specific, the objective of this study is to demonstrate how a DES modeling approach can help understand underlying mechanisms of changes in arbors over the course of the hair cycle. In contrast to the prior computational modeling efforts, that presented herein takes on a bottom up approach, with encoded probability rules for each specific constituent as the parent end organ goes through the hair cycle. Policies are a combination of conditional and probabilistic rules. Unlike the computational model, each Merkel cell, terminal neurite branch and heminode relating to a particular end organ was examined individually, and rules governing their addition and deletion were reflective of hypotheses regarding biological characteristics. This bottom-up approach, which models end organs, heminodes, and terminal neurite branches as different entities, allowed us to refine the governing policies and estimate optimal parameters that play a role in the remodeling processes. The Merkel cells are modeled as an attribute of terminal branches that affects the policies and parameters.